假设一堆人申请一个秘书岗位，而你是面试官，你的目标是从这堆申请人中遴选出最佳人选。你不知道如何给每一名申请人评分，但是可以轻松地判断哪一名申请人更加优秀。（用数学语言来表述，就是说你只能看到序数，即申请人相互比较的排名，但是无法看到基数，即在一般性评分标准下的得分。）你按照随机顺序，每次面试一名申请人。你随时可以决定将这份工作交给其中一人，而对方只能接受，于是面试工作就此结束。但是，一旦你否决其中一名申请人，就不能改变主意再回头选择他。

在选择时，遴选程序停止过早或者过晚都会导致不理想的结果。停止过早，最优秀的申请人还没有得到亮相的机会；停止过晚，就说明你在为一位根本不存在的更优秀的申请人保留这份工作。那么，我们到底该怎么办？凭直觉，我们可以找到几种应对的办法。例如，当第三次（或者第四次）出现胜过前面所有的申请人时，就把工作机会交给他。或者，在连续多个申请人都不理想的情况下，一旦出现一名目前为止最优秀的人选，就毫不犹豫地接受他。

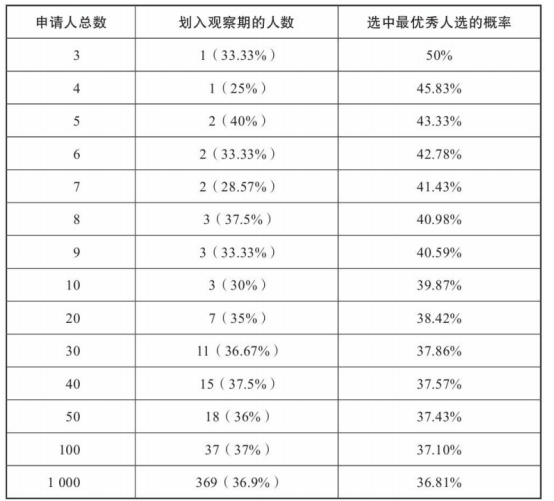
但是，事实证明，所有这些相对来说似乎有道理的策略都算不上是最明智的做法。事实上，效果最佳的做法是接受所谓的“摸清情况再行动准则 ”（look-then-leap rule）：事先设定一个“观察”期，在这段时间里，无论人选多么优秀，都不要接受他（也就是说，你的任务就是考察目标，收集数据）。“观察”期结束之后，就进入了“行动”期。此时，一旦出现令之前最优秀申请人相形见绌的人选，就立即出手，再也不要犹豫了。 如果有三名申请人，随机选择一名申请人，得到理想结果的概率是1/3，也就是33%。有两名申请人时，我们没有办法取得比碰运气更好的结果。那么，在有三名申请人时，会怎么样？事实证明，我们可以取得更理想的结果，而其中的关键就在第二场面试。在面试第一名申请人时，我们没有任何信息——她肯定是目前最优秀的申请人。在面试第三名申请人时，我们没有任何能动性——我们只能将工作机会交给这名申请人，因为我们已经拒绝了其他人的申请。但是，在面试第二名申请人时，我们既掌握了一些信息，又有一定的能动性——我们知道她与第一名申请人相比孰优孰劣，同时我们既可以接受她，也可以拒绝她。如果她比第一名申请人优秀，我们接受她，反之就拒绝她，那么会产生什么样的结果？事实上，在有三名申请人时，这是最理想的方案。随着申请人数不断增加，观察与行动之间的分界线正好处在全部申请人37%的位置，从而得出了37%法则：在考察前37%的申请人时，不要接受任何人的申请；然后，只要任何一名申请人比前面所有人选都优秀，就要毫不犹豫地选择他。

What:这个片段讲的是如何做出最优概率更高的选择，即37%法则。

Why：不这么做的坏处，做选择的时候，停止过早，最优选可能还没出现，停止过晚，错过最优选，用原文的话说就是“在为一位根本不存在的人保留职位”。好处是，运用37%法则，做出最优选择的概率更高。

Where：适用于无法获知全信息的时候，无法重复选择，有进无退时。比如租房、买房，相亲、选择结婚时间也可以。不适用于可以知道全信息的场景，或者有明确的评判标准，比如分数，比如速度等，就像我把要面试20个人全部面试完再给结果，或者考试选择分数最高的，或者就要腿最长。

How：三个步骤

1、预设数据总量。注意，这个总量可以是你的心理预期。预设数据总量，有总量才能设置37%。比如公司准备招一个人，但是总共邀请了30个人来参与面试。前提是需要当场给出结果，不能回头选择。

2、收集数据。前37%作为样本数据进行观察，不做选择。30个人，前37%是多少？请拿出你的手机，点开计算器，然后口算。11.1，四舍五入，这11个人都不要。

3、行动。37%之后，一旦出现比前面都更优的选择，不要犹豫，是它是他就是她。从第12个人开始，一旦出现了比前面都更优秀的人，立刻选择。

我分享一个我的案例。前年我准备在重庆买房子，当时正是重庆房事火热的时候。我一一看过了20来套，准备入手，位置户型价格都不错，电话打过去，哦豁，没了。然后又想，后面肯定还有更好的房子，又继续看，过了一个月，哦豁，房价涨了。多么痛的领悟。如果用37%法则我会怎么做？第一步，先预设总量，设置个50套，再多了也累也耗时间；第二步，收集数据，前37%，19套光看不买，作为样本观察；第三步，37%之后，一旦遇上更好的，立刻下手。

A1

拆书家提问设计：（逐字稿）

现在，请每位同学回忆最近一个月或者一年经历过的或者见过的，做选择时，因为无法全知信息，而不知该如何做出合理选择的实例，比如大学毕业签三方，求职收到很多offer不知道怎么选，停车位选择等等，小组内分享，3分钟。3分钟后我请一位同学来分享。

学习者案例记录：

典妈：2021年和朋友一起为朋友的孩子申请美国某大学本科专业，该学校的录取标准除了分数之外还有另外6个无法用数据衡量的标准，由于不清楚该学校除硬性指标外的录取原则，不知道学校到底是如何从上千的申请者中选出那么寥寥数十位的，因此不知道该如何做才可以增加申请成功率。经历了各种煎熬，庆幸的是，最后申请成功了。2022年，她也要为自己的孩子申请该所大学的专业了。今天听到37%法则的分享，意识到该学校有可能会用37%法则在选择申请者，所以她想如何反向应用37%法则。

A2

拆书家提问设计：（逐字稿）

听完今天关于37%法则的分享，现在请大家拿出便签，写下如何运用37%法则规划以后可能遇到的类似这种无法全知信息又需要做出选择的场景，单身的规划一下相亲怎么选对象，没结婚的规划一下啥时候结婚（具体、可衡量、时限）。

学习者案例记录：

孔：在重庆工作，租住某地。房子合约到期，马上要重新租房了，现在运用37%法则进行租房规划。时限是1个月内，租一套满意的房子，一室一厅，价格1500每月以内，到公司通勤时间半个小时以内。

第一步，预设看房数量20套。

第二步，收集数据，前37%即7套作为样本，比较价格，位置等等，不做选择。

第三步，行动，37%之后，一旦出现比前面7套都更好的选择，立刻行动。